
25 to 100, given that 100 only has one sig fig and therefore we don't trust even the two zeros, can you really say you have 100.25? That would be saying that you were sure the first 100 was, in fact, 100.00! If the 100 had five sig figs, why didn't someone say so? Multiplication also has rules about this. When scientists are calculating with sig figs, the precision of the result should reflect the uncertainty of the numbers that went into it. Our next question needs to be, "What happens to the number of sig figs when we perform calculations?" This is not the E that means error.īe careful! It's easy to make the following common mistake: Remember that EE -times ten to the - is not the same as ^ - "to the"!Ĥ EE 1 equals 40 (as does 4 * 10^1), not 4!

Note that when you type the EE key, most calculators simply print "E"! Do not be alarmed by this. Most calculators have an "EE" button, to help you out. When you are using your calculator, typing "something times ten to the something" over and over again gets to be a pain. Here is one way to type these numbers into your calculator:
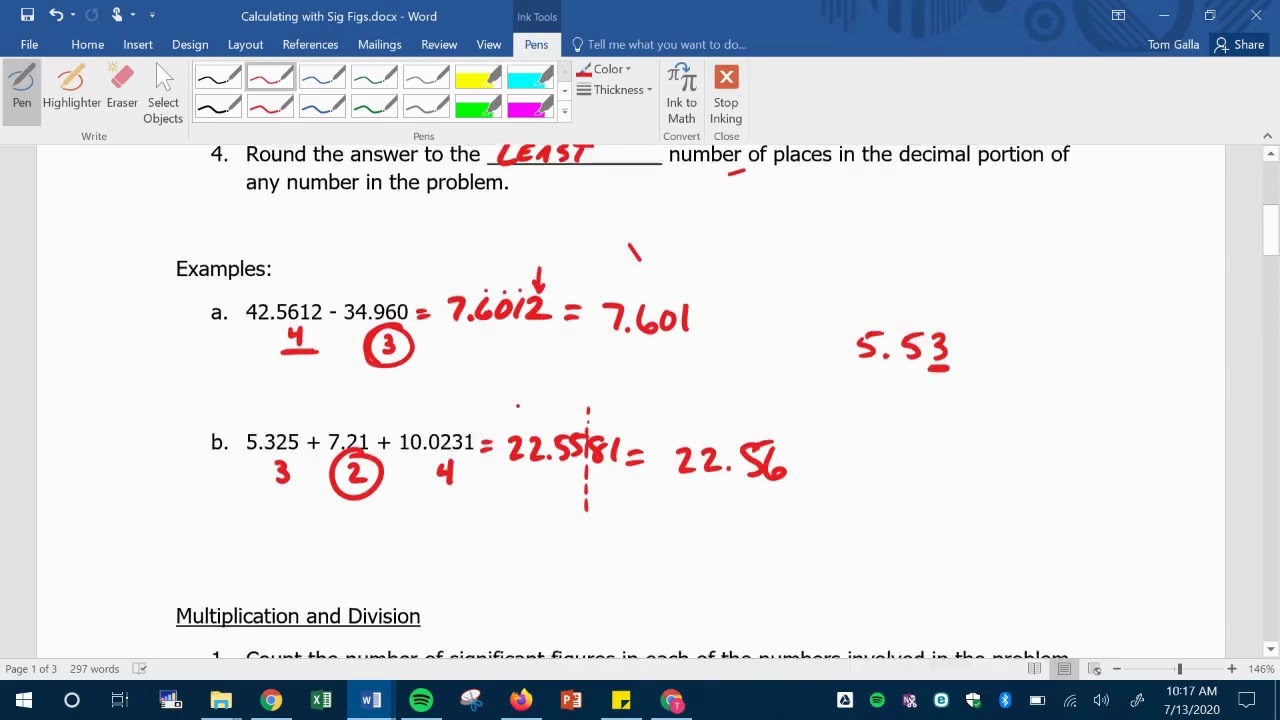
SIG FIG HOW TO
In the fifth example, we have finally seen how to represent 100 with exactly two sig figs. In the fourth example the extrazeros (on the right!) are used to indicate that we have extra certainty. In the third example, the extraneous decimal placeis used to mean we are certain of all three digits. See the differences? In the first and second example, the zerosare really only place holders. Here are some numbers in scientific notation to study: Scientific notation makes sure that everything but the first digit of a number is after the decimal place and therefore either signigicant or not used. Scientists use scientific notationto handle this problem. So, how does a scientist indicate that two of the digitsin 100 are significant? We can't put in a decimal point alone to make 100. Zeros that only hold places are not considered to be significant. So does the number 130, but 10 and 100 only have one "sig fig" as written. The number 1.0 also has two significant digits. The number "10." is said to have two significant digits, or significant figures, the 1 and the 0. The use of the decimal point indicates that the scientist is sure of both digits to some reasonable degree - it is 10.something, not 11 or 9, even though rounding both of these numbers to one digit gives 10. This is actually different from saying that they measured "10" cm. They might say, for example, that they measured "10." cm. Scientists put only the digits they can reasonably be certain of in their numbers.

However, this notation gets cumbersome fast.
SIG FIG PLUS
This can be stated as "We measured ten, plus or minus one", and often scientists douse these terms. When scientists measure a quantity, they actually measure two pieces of information-the value they think they have measured, and the uncertainty.


 0 kommentar(er)
0 kommentar(er)
